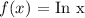Explain the behavior of f(x)= ln (x-a) when x=a. Give values to x and a such that x-a=0

Question

asked Sep 24, 2023 130k views

1 Answer

Parth Dave · Answer 1 · 2023-10-01T01:54:52+0000

SOLUTION:

Step 1:

In this question, we are given the following:

Explain the behavior of :

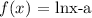
$f(x)\text{ = ln\lparen x-a\rparen}$

when x=a.

Give values to x and a such that:

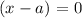
$(x-a)\text{ = 0}$

Step 2:

The graph of the function:

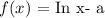
$f(x)\text{ = In \lparen x- a \rparen}$

are as follows:

Step-by-step explanation:

From the graph, we can see that the function:

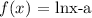
$f(x)\text{ = ln\lparen x-a\rparen}$

is a horizontal translation, shift to the right of its parent function,

$f(x)\text{ = In x}$