Question

Use U-Subscription to solve the following polynomial. Compare the imaginary roots to the code breaker guide. Hi this is a project and this is one of the questions, I have the guide so ignore the code piece part.

Answer 1

We will substitute the variable x with the variable u using the following relation:

`u=x^2`

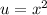
Then, we can convert the polynomial as:

`4x^4+2x^2-12=4u^2+2u-12`

We can use the quadratic equation to calculate the roots of u:

`\begin{gathered} u=\frac{-2\pm\sqrt[]{2^2-4\cdot4\cdot(-12)}}{2\cdot4} \\ u=\frac{-2\pm\sqrt[]{4+192}}{8} \\ u=\frac{-2\pm\sqrt[]{196}}{8} \\ u=(-2\pm14)/(8) \\ u_1=(-2-14)/(8)=-(16)/(8)=-2 \\ u_2=(-2+14)/(8)=(12)/(8)=1.5 \end{gathered}`

We have the root for u: u = -2 and u = 1.5.

As u = x², we have two roots of x for each root of u.

For u = -2, we will have two imaginary roots for x:

`\begin{gathered} u=-2 \\ x^2=-2 \\ x=\pm\sqrt[]{-2} \\ x=\pm\sqrt[]{2}\cdot\sqrt[]{-1} \\ x=\pm\sqrt[]{2}i \end{gathered}`

For u = 1.5, we will have two real roots:

`\begin{gathered} u=1.5 \\ x^2=1.5 \\ x=\pm\sqrt[]{1.5} \end{gathered}`

Then, for x, we have two imaginary roots: x = -√2i and x = √2i, and two real roots: x = -√1.5 and x = √1.5.

Answer:

Let u = x²

Equation using u: 4u² + 2u - 12

Solve for u: u = -2 and u = 1.5

Solve for x: x = -√2i, x = √2i, x = -√1.5 and x = √1.5

Imaginary roots: x = -√2i and x = √2i

Real roots: x = -√1.5 and x = √1.5