We have , that measure of the side of the square is x
Therefore
l=26-2x
w=20-2x
h=x
Therefore the Volume function is
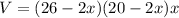
Then we simplify

6.In the context of obtaining a Volume we can't have negative numbers for x and for the function by observing the graph
Domain
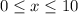
Therefore for the range
![0\: 7.<p>Because we have a polynomial</p><p></p><p>the domain without the constrain</p>[tex]-\infty\: the range without the constrain<p></p>[tex]-\infty\: 8.<p>Since the leading term of the polynomial is 4 x^(3), the degree is 3, i.e. odd, and the leading coefficient is 4, i.e. positive. This means</p>[tex]\begin{gathered} x\to-\infty,\text{ }f(x)\to-\infty \\ x\to\infty,f(x)\to\infty \end{gathered}]()