Question

13. A 640 kg of a radioactive substance decays to 544 kg in 13 hours. A. Find the half-life of the substance. Be sure to show your work including the formulas you used. Round to the nearest tenth of an hour. Only solutions using formulas from the 4.6 lecture notes will receive credit.B. How much of the substance is present after 3 days? Be sure to show the model you used.C. How long does it take the substance to reach 185 kg? Be sure to show your work.

Answer 1

EXPLANATION

The equation for half-life is given by the following formula:

`H=(t\cdot\ln(2))/(\ln((A_0)/(A_t)))`

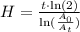
Replacing terms:

`H=(t\cdot\ln(2))/(\ln((A_0)/(A_t)))=(13\cdot\ln(2))/(\ln((640)/(544)))=(9.0109)/(0.1625)=55.45`

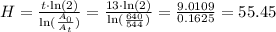
The half-life time is H =55.4 hours.

B) After three days, that is, 72 hours, the amount of substance will be given by the following relationship:

`A=A_o\cdot e^{-((\ln2)/(H))t}=640\cdot e^{-((\ln2)/(55.4))\cdot72}=640\cdot e^(-0.90084)`

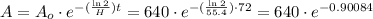
Multiplying terms:

`A=640\cdot0.4062=259.96\text{ Kg}`

There will be 259.96 Kg after 3 days.

C) In order to compute the number of days that will take to the substance to reach a concentration equal to 185 Kg, we need to apply the following formula:

`t=(\ln ((A)/(A_o)))/(-(\ln (2))/(t(1)/(2)))`

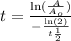
Replacing terms:

`t=(\ln ((185)/(544)))/(-(\ln (2))/(55.45))=(-1.0785)/(-0.0125)=(1.0785)/(0.0125)=86.28\text{ hours}`

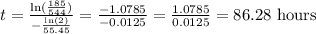
It will take 86.28 hours to the substance to reach 185 Kg.