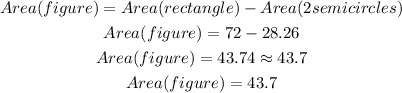Question

Find the area of the figure below, composed of a rectangle with two semicircles removed.

Answer 1

This is a composite shape composed of a rectangle with two semicircles removed. The area will be calculated by subtracting the area of the two semicircles from the area of the rectangle

The area of a rectangle is given by:

`\begin{gathered} Area(rectangle)=length\cdot width \\ length=12 \\ width=6 \\ Area(rectangle)=12\cdot6=72 \\ Area(rectangle)=72 \end{gathered}`

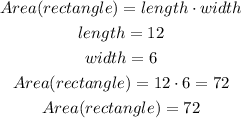
The area of the two semicircles is given by:

`\begin{gathered} Area(2semicircles)=2((1)/(2)\pi r^2) \\ Area(2semicircles)=\pi r^2 \\ r=(diameter)/(2)=(6)/(2)=3 \\ Area\mleft(2semicircles\mright)=\pi\cdot3^2=3.14\cdot9=28.26 \\ Area\mleft(2semicircles\mright)=28.26 \end{gathered}`

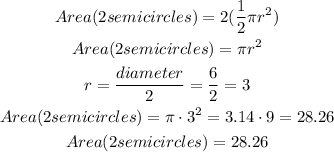
Therefore, the area of the figure is:

`\begin{gathered} Area(figure)=Area(rectangle)-Area(2semicircles) \\ Area(figure)=72-28.26 \\ Area(figure)=43.74\approx43.7 \\ Area(figure)=43.7 \end{gathered}`