Given:
A scientist has 5% and a 10% acid solution in his lab.
He needs 270 milliliters of a 20% acid solution.
To find the amount of 25% solution and how many milliliters of the 10% solution should the scientist mix to make the 20% solution:
Here,
The dearer percentage is 25%.
The cheaper percentage is 10%.
The mean percentage is 20%.
Using the mixture and allegation method,
The ratio of the litters of cheaper (10% solution) to dearer value (25% solution) is,
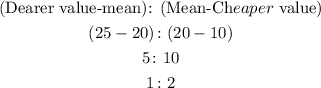
So, the number of liters to be taken from 10% solution is,
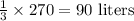
So, the number of liters to be taken from 25% solution is,
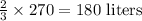
Hence, the answer is