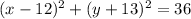Answer:
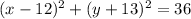
Step-by-step explanation:
Given:
• Center: (12,-13)
,
• Point on circle: (18, -13)
First, we find the length of the radius.
![\begin{gathered} r=\sqrt[]{(18-12)^2+(-13-(-13)_{})^2} \\ =\sqrt[]{(6)^2} \\ r=6\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i6fvgrdk6ub9p0kwlc75rovunwvec7iizj.png)
The general equation of a circle is given as:

Substituting the centre, (h,k)=(12,-13) and r=6, we have:

The equation of the circle is: