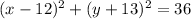Question

use the information provided to write the equation of each circle. center: (12,-13)point on circle: (18, -13)

Answer 1

`(x-12)^2+(y+13)^2=36`

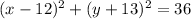
Step-by-step explanation:

Given:

• Center: (12,-13)

,

• Point on circle: (18, -13)​

First, we find the length of the radius.

`\begin{gathered} r=\sqrt[]{(18-12)^2+(-13-(-13)_{})^2} \\ =\sqrt[]{(6)^2} \\ r=6\text{ units} \end{gathered}`

The general equation of a circle is given as:

`(x-h)^2+(y-k)^2=r^2`

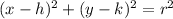
Substituting the centre, (h,k)=(12,-13) and r=6, we have:

`\begin{gathered} (x-12)^2+(y-(-13))^2=6^2 \\ (x-12)^2+(y+13)^2=36 \end{gathered}`

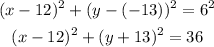
The equation of the circle is:

`(x-12)^2+(y+13)^2=36`