We were given a principal to invest ($14,000) in a timespan of 2 years, and we need to choose between applying it on an account that is compounded montlhy at a rate of 6%, and one that is compounded continuously at a rate of 5.88%. To solve this problem, we need to calculate the final amount on both situations, and compare them.
The expression used to calculate the amount compounded monthly is shown below:

Where A is the final amount, P is the invested principal, r is the interest rate and t is the elapsed time.
The expression used to calculate the amount compounded continuously is shown below:
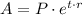
Where A is the final amount, P is the invested principal, r is the interest rate, t is the elapsed time, and "e" is the euler's number.
With the two expressions we can calculated the final amount on both situations, this is done below:
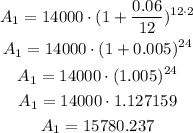
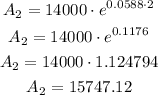
The first account, that is compounded monthly yields a return of $15780.24, while the second one that is compounded continuously yields a return of $15747.12, therefore the first account is the one that yield the larger amount in 2 years.