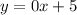Question

What is the equation, in slope-intercept form, of a line that passes through the points(-8,5) and (6,5)?

Answer 1

Given the points (-8,5) and (6,5), we can find the equation of the line first by finding the slope with the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

in this case, we have the following:

`\begin{gathered} (x_1,y_1)=(-8,5) \\ (x_2,y_2)=(6,5) \\ \Rightarrow m=(5-5)/(6-(-8))=(0)/(6+8)=0 \\ m=0 \end{gathered}`

since the slope is m = 0, we have that the line is a horizontal line that goes through the points (-8,5) and (6,6), then, the equation of the line is:

`y=5`

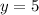
in slope-intercept form the equation would be:

`y=0x+5`