Question

A number from 1-40 is chosen at random. Find each probability.1. Pleven | at least 12)2. P(perfect square | odd)3. P(less than 25 | prime)4. P(multiple of 3 | greater than 15)

Answer 1

Given:

Numbers from 1 - 40

Let's find the probability of:

Pleven | at least 12)

Where:

Even numbers = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40 = 20 numbers

Even numbers that are at least 12 = 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40 = 15 numbers.

Numbers that are at least 12 = 29 numbers

Therefore, to find the probability, we have:

`P(even|atleast12)=\frac{P(even\text{ and at least 12\rparen}}{P(at\text{ least 12\rparen}}`

Where:

`\begin{gathered} P(even\text{ and at least 12\rparen = }(15)/(40)=0.375 \\ \\ P(at\text{ least 12\rparen= }(29)/(40)=0.725 \end{gathered}`

Therefore, we have:

`\begin{gathered} P(even|atleast12)=(0.375)/(0.725) \\ \\ P(even|atleast12)=0.52 \end{gathered}`

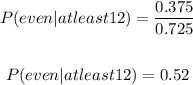
Therefore, the probability that a number chosen at random is even given that it is at least 12 is 0.52

ANSWER:

0.52