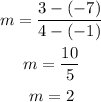Answer:
From the above options, the only table that have the same slope as the given line in the equation (m=2) is Table C.
Step-by-step explanation:
Given the equation;
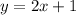
The slope of the above line is;
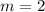
From the given options, let us find the table that has the same slope as the above equation;
A.
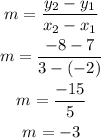
B.
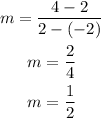
C.
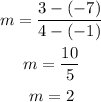
D.
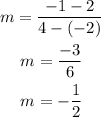
From the above options, the only table that have the same slope as the given line (m=2) is Table C.