A line has the given slope m and passes through the first point listed in the table. Complete the table so that each point on the table lies on the line.

Question

asked Jan 28, 2023 55.9k views

1 Answer

Aleafonso · Answer 1 · 2023-02-03T17:23:44+0000

A line can be written as an equation in the slope-intercept form:

Where m is the slope and b is the y-intercept.

We know the slope:

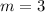
The y-intercept is the y value of the graph where it intercepts the y-axis, which happens when x = 0.

We know that the point x = 0 and y = 3 is on the line and, since the value of x is 0. the y value is the y-interceot, so:

Thus, we have the equation:

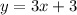
To calculate the other points, we just need to substitute their x values and get their y values:

x = 1:

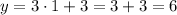
$y=3\cdot1+3=3+3=6$

So, when x = 1, y = 6

x = 2:

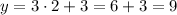
$y=3\cdot2+3=6+3=9$

So, when x = 2, y = 9.

x = 3:

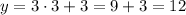
$y=3\cdot3+3=9+3=12$

So, when x = 3, y = 12;

So, the complete table is:

x | 0 | 1 | 2 | 3

y | 3 | 6 | 9 | 12