Question

Help I am not sure how to do this number 8

Answer 1

Answer: The temperature of the gas sample under the conditions given is 30.313 K

Step-by-step explanation:

The question requires us to determine the temperature, in Kelvins, of a C2H6 gas sample with the following mass, volume and pressure:

mass of C2H6 = m = 561.51g

volume of gas = V = 47.048L

pressure of gas = P = 100.03 kPa

To solve this problem, we can apply the equation of ideal gases rearranged to calculate the temperature, as shown below:

`PV=nRT\rightarrow T=(PV)/(nR)`

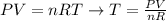
where T is the temperature we want to calculate, P corresponds to the pressure of the gas, V is its volume, n is its number of moles and R is the constant of gases (8.314 kPa.L/mol.K).

Note that the only valye that was not provided by the question was the number of moles. We can determine the number of moles n considering the mass of the sample given (561.51g) and the molar mass of the gas C2H6, which we can determine from the atomic masses of C and H.

The atomic masses of C and H are 12.011 and 1.0078 amu, thus we can calculate the molar mass of C2H6 as:

`molar\text{ mass \lparen C}_2H_6)=2*12.011+6*1.0078=30.069g/mol`

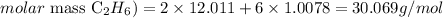
Now that we know the mass of the gas sample (561.51 g) and the molar mas of the gas (30.069 g/mol), we can determine the number of moles of gas as it follows:

`\begin{gathered} number\text{ of moles = }\frac{mass\text{ \lparen g\rparen}}{molar\text{ mass \lparen g/mol\rparen}}\rightarrow n=(m)/(M) \\ \\ n=(561.51g)/(30.069g/mol)=18.674mol \end{gathered}`

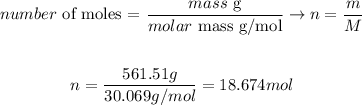
Therefore, the number of moles of C2H6 gas that we need to consider is 18.674 moles.

Next, we can apply the equation of ideal gases to calculate the temperature of the gas:

`\begin{gathered} T=(PV)/(nR) \\ \\ T=((100.03kPa)*(47.048L))/((18.674mol)*(8.314kPa.L/mol.K))=30.313K \end{gathered}`

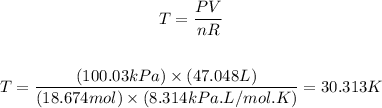
Therefore, the temperature of the gas sample under the conditions given is 30.313 K.