In general, the exponential growth function is given by the formula below
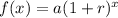
Where a and r are constants, and x is the number of time intervals.
In our case, n=0 for 1960; therefore, 1968 is n=8,
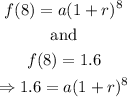
And 1976 is n=16
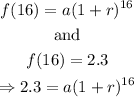
Solve the two equations simultaneously, as shown below
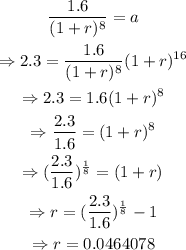
Solving for a,
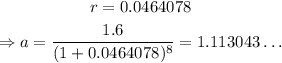
a) Thus, the equation is

b) 1960 is n=0; thus,
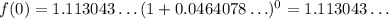
The answer to part b) is $1.113043... per hour
c)1996 is n=36
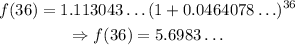
The model prediction is above $5.15 by $0.55 approximately. The answer is 'below'