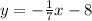Question

Find the equation of the line with the given properties. Express the equation in general form or slope-intercept form.

Answer 1

To asnwer this questions we need to remember that two lines are perpendicular if and only if their slopes fullfil:

`m_1m_2=-1`

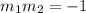
Now to find the slope of the line

`-7x+y=43`

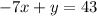
we write it in slope-intercept form y=mx+b:

`\begin{gathered} -7x+y=43 \\ y=7x+43 \end{gathered}`

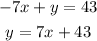
from this form we conclude that this line has slope 7.

Now we plug this value in the condition of perpendicularity and solve for the slope of the line we are looking for:

`\begin{gathered} 7m=-1 \\ m=-(1)/(7) \end{gathered}`

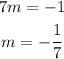
Once we hace the slope of the line we are looking for we plug it in the equation of a line that passes through the point (x1,y1) and has slope m:

`y-y_1=m(x-x_1)`

Plugging the values we know we have that:

`\begin{gathered} y-(-7)=-(1)/(7)(x-(-7)) \\ y+7=-(1)/(7)(x+7) \\ y+7=-(1)/(7)x-1 \\ y=-(1)/(7)x-8 \end{gathered}`

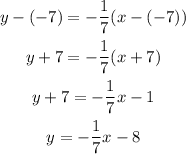
Therefore the equation of the line is:

`y=-(1)/(7)x-8`