Okay, here we have this:
Considering the provided information we obtain the following:
a)
Replacing in the Compound Interest formula we obtain the following:
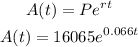
b)
After 1 year (t=1):
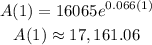
We obtain that after one year the balance is aproximately $17,161.06.
After 2 years (t=2):
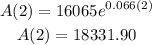
We obtain that after two years the balance is aproximately $18,331.90
After 5 years (t=5):
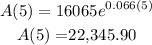
We obtain that after five years the balance is aproximately $22,345.90.
After 10 years (t=10):
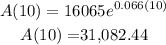
We obtain that after ten years the balance is aproximately $31,082.44.
c)
In this case the doubling time will be when she has double what she initially had, that is: $16,065*2=$32130, replacing in the formula:
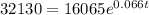
Let's solve for t:
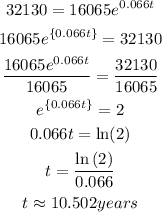
Finally we obtain that the doubling time is approximately 10.502 years or about 10 years 6 months.