Question

4. You are making guacamole for a familygathering. Your first trip to the store, youpurchased 5 avocados and 3 pounds of tomatoesfor $13.30. The head count changed, and youwent back for an additional 3 avocados and 8pounds of tomatoes, spending another $22.55.What is the price per avocado and pound oftomatoes?

Answer 1

hello

to solve this question, we need to write an equation expressing the word problem and solve for the price of each item.

let x represent the cost of avocados

let y represent the cost of tomatoes

`\begin{gathered} 5x+3y=13.30\ldots\text{.equation 1} \\ 3x+8y=22.55\ldots\text{.equation 2} \end{gathered}`

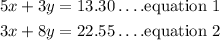
from equation 1, let's make xthe subject of formula

`\begin{gathered} 5x+3y=13.30 \\ 5x=13.30-3y \\ \text{divide both sides by 5 to solve for x} \\ x=(13.30-3y)/(5) \\ \text{this is equation 3} \end{gathered}`

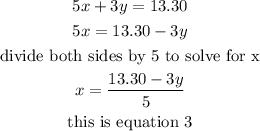
put equation 3 into equation 2

`\begin{gathered} 3x+8y=22.55 \\ 3((13.30-3y)/(5))+8y=22.55 \\ (39.9-9y)/(5)+8y=22.55 \\ \text{solve for y} \\ (39.9-9y+40y)/(5)=22.55 \\ (39.9+31y)/(5)=22.55 \\ 39.9+31y=22.55*5 \\ 39.9+31y=112.75 \\ 31y=112.75-39.9 \\ 31y=72.85 \\ y=(72.85)/(31) \\ y=2.35 \end{gathered}`

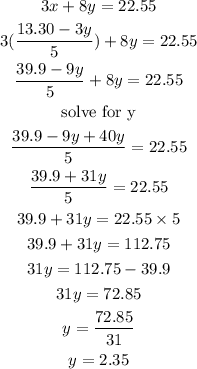
since y = 2.35, let's put that in either equation 1 or 2

from equation 2

3x + 8y = 22.55

put y = 2.35 and solve for x

`\begin{gathered} 3x+8y=22.55 \\ y=2.35 \\ 3x+8(2.35)=22.55 \\ 3x+18.8=22.55 \\ 3x=22.55-18.8 \\ 3x=3.75 \\ x=(3.75)/(3) \\ x=1.25 \end{gathered}`

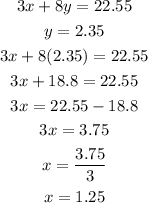
from the calculations above, the price per avocado and pound of tomatoes are $1.25 and $2.35 respectively