Question

A vehicle factory manufactures cars. The unit cost C (the cost in dollars to make each car) depends on the number of cars made. If x cars are made, thenthe unit cost is given by the function C(x) = 0.5x? - 260x +53,298. How many cars must be made to minimize the unit cost?Do not round your answer.

Answer 1

Okey, here we have the following function:

`C(x)=0.5x^2-260x+53298`

Considering that "a" is a positive coefficient, then it achieves the minimum at:

`x=-(b)/(2a)`
`\begin{gathered} x=-((-260))/(2(0.5)) \\ =(260)/(1) \\ =260 \end{gathered}`

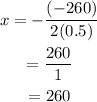
Now, let's find the minimal value of the quadratic function, so we are going to replace x=260, in the function C(x):

`\begin{gathered} C(260)=0.5(260)^2-260(260)+53298 \\ C(260)=0.5(67600)-67600+53298 \\ =33800-67600+53298 \\ =19498 \end{gathered}`

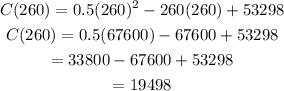
Finally we obtain that the number of cars is 19498.