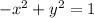
The intercepts for a function can be on either of the two axis, y or x.
when finding the intercepts of x, means that y = 0
when finding the intercepts of y, means that x = 0
finding the x intercepts
![\begin{gathered} -x^2+(0)^2=1 \\ -x^2=1 \\ x^2=-1 \\ x=\sqrt[]{-1} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2p7ihu2mu0llfx1eh3n8s12ubluju94v2i.png)
since the solution for the square root of -1 has not any solution on the real numbers, we can say that there is no intercept over the x axis.
finding the y intercepts
![\begin{gathered} -(0)^2+y^2=1 \\ y^2=1 \\ y=\pm\sqrt[]{1} \\ y=1;y=-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ggk52mbwuuq3c1xemnuyooyrgdwn5kj248.png)
there are 2 intercepts on the y axis, these are at y=1 and y=-1
information can be proven by graphing the function