The Solution:
The correct answer is 67 degrees.
Given the rhombus below:
We are required to find the measure of angle PRZ.
Considering trianglePRZ, we can apply the law of cosine to the angle of interest, which is, angle PRZ.
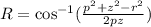
In this case,
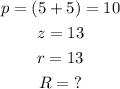
Substituting these values in the formula, we get
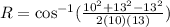
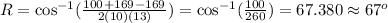
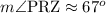
Therefore, the correct answer is 67 degrees.