Question

9. The Elite Vacuum Company has determined its cost for making vacuums to beC = 24V + 1000, where C is the cost in dollars and V is the number of vacuums.If the cost must be between $49,000 and $121,000, how many vacuums can they makeper week? (You must set up and solve an inequality.)

Answer 1

We are given the relationship between the cost in dollars (C) and the number of vacuums (V) to be:

`C\text{ = 24V + 1000}`

From the constraint, we have that the cost(C) must be greater than $49000 and less than $121000

Writing this as inequality:

`\begin{gathered} 24V\text{ + 1000 }\ge\text{ 49000 } \\ 24V\text{ + 1000 }\leq\text{ 121000} \end{gathered}`

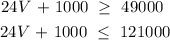
Solving the linear inequalities for V:

`\begin{gathered} 24V\text{ + 1000 }\ge\text{ 49000} \\ 24V\text{ }\ge\text{ 49000 - 1000} \\ 24V\text{ }\ge\text{ 48000} \\ \text{Divide both sides by 24} \\ (24V)/(24)\text{ }\ge\text{ }(48000)/(24) \\ V\text{ }\ge\text{ 2000} \end{gathered}`

Similarly for the second inequality:

`\begin{gathered} 24V\text{ + 1000 }\leq\text{ 121000} \\ 24V\text{ }\leq121000\text{ - 1000} \\ 24V\text{ }\leq\text{ 120000} \\ \text{Divide both sides by 24} \\ (24V)/(24)\text{ }\leq\text{ }(120000)/(24) \\ V\text{ }\leq5000 \end{gathered}`

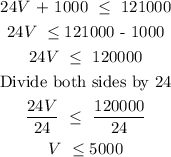
Hence, the number of vacuums they can make per week can be between 2000 and 5000 or in inequality:

`2000\text{ }\leq\text{ V }\leq\text{ 5000}`

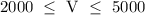
Answer:

Between 2000 and 5000 vacuums