ANSWER
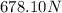
Step-by-step explanation
Parameters given:
Coefficient of static friction, μs = 0.105
Force, F = 71.2 N
The minimum force required to set the sled moving must be equal to the frictional force acting on the sled.
The frictional force is given mathematically as:
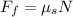
where N = normal force
Since the force required is equal to the frictional force, we have that:
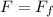
Therefore:
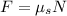
Solve for N:
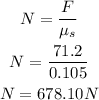
That is the normal force.