Question

A sailboat starts from rest and accelerates at a rate of 0.13 m/s? over a distance of 344 m.(a) Find the magnitude of the boat's final velocitym/s (b)find the time it takes the boat to travel this distance

Answer 1

We know that

• It starts from rest. (The initial velocity is zero).

,

• The acceleration rate is 0.13 m/s^2.

,

• The distance covered is 344 m.

To find the magnitude of the boat's final velocity, we have to use the following formula.

`v^2_f=v^2_0+2ad`

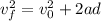
Let's use the given magnitudes.

`\begin{gathered} v^2_f=0^2+2(0.13((m)/(s^2)))(344m) \\ v^2_f=89.44((m^2)/(s^2)) \\ v_f=\sqrt[]{89.44((m^2)/(s^2))} \\ v_f\approx9.46((m)/(s)) \end{gathered}`

(a) Therefore, the final velocity is 9.46 meters per second.

Now, to find the time it takes the boat to travel this distance, we use the following formula.

`d=v_0\cdot t+(1)/(2)at^2`

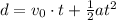
Using the given magnitudes, we have the following.

`344m=(1)/(2)(0.13((m)/(s^2)))t^2`

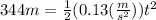
Let's solve for t.

`\begin{gathered} t=\sqrt[]{(2\cdot344m)/(0.13((m)/(s^2)))} \\ t=\sqrt[]{(688m)/(0.13)}\sec \\ t\approx72.75\sec \end{gathered}`

(b) Therefore, it takes 72.75 seconds.