We will make use of the z-score to calculate the probability. The z-score is calculated using the formula:

where x is the score, μ is the mean, and σ is the standard deviation.
From the question, we have the following parameters:

Therefore, we have the z-score to be:
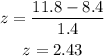
Using a calculator, we can get the probability value to be:

The probability is 0.9925 or 99.25%.