Question

a) your one friend and their bumper boat (m = 210 kg) are traveling to the left at 3.5 m/s and your other friend and their bumper boat (m = 221 kg) are traveling in the opposite direction at 1.8 m/s. The two boats then collide in a perfectly elastic one-dimensional collision. How fast is your first friend and their boat moving after the collision?b) after the collision, a constant drag force between the water and the boat causes your first friends boat to come to a stop. If the boat travels 2.7 m before stopping, what is the magnitude of the constant drag force?

Answer 1

a) 1.757 m/s

b) 119.91 N

Explanation:

Given:

Mass 1 (m1) = 210 kg

Initial speed 1 (u1) = 3.5 m/s

Mass 2 (m2) = 221 kg

Initial speed (u2) = 1.8 m/s

We make a sketch of the situation:

a)

We make a momentum balance by taking into account the conservation of momentum:

`\begin{gathered} m_1u_1-m_2u_2=m_1v_1+m_2v_2 \\ \\ v_2=(m_1u_1-m_2u_2-m_1v_1)/(m_2)\rightarrow(1) \end{gathered}`

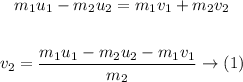
Now an energy balance taking into account the conservation of energy, as follows:

`\begin{gathered} (1)/(2)m_1(u_1)^2+(1)/(2)m_2(u_2)^2=(1)/(2)m_1(v_1)^2+(1)/(2)m_2(v_2)^2 \\ \\ m_1\left(u_1\right)^2+m_2\left(u_2\right)^2=m_1\left(v_1\right)^2+m_2\lparen v_2)^2\rightarrow(2) \end{gathered}`

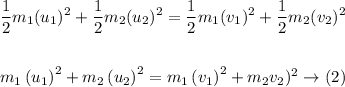
Now, we substitute equation (1) in (2) and we get the following:

b)

We use the following formula to determine the force:

`\begin{gathered} v^2=u^2+2as \\ \\ \text{ Wee replacing:} \\ \\ (1.756)^2=0^2+2\cdot a\cdot2.7 \\ \\ a=0.003375\text{ m/s}^2 \\ \\ \text{ Therfore:} \\ \\ F=m\cdot a=210\cdot0.571=119.91\text{ N} \end{gathered}`