Given data,
The initial velocity of the body is zero.
The distance travelled by the rescuer upto the height of 30 m from the water surface is,
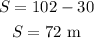
The final velocity of the rescuer at the height 30 m is,
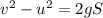
where g is the acceleration due to gravity.
Substituting the known values,
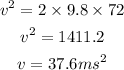
Thus, the kinetic energy of the rescuer is,
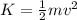
Substituting the known values,
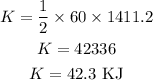
Thus, the kinetic energy of the rescuer is 42.3 KJ and speed of the rescuer is 37.6 meter per second square.