Question

14. A can of vegetables has a paper label that covers the lateral surface are can, 4 in. 2.6 in. What is the lateral surface area of the can onded to the

Answer 1

We will have that the lateral area will be the following:

*First, we can see that if we were to cut a straight vertical line and unfold the label, we would get a rectangle, thus the surface area of the label will be given by:

`S_A=h\cdot C`

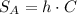
Here h is the height of the label and C is the circumference of the base, that is:

`S_A=h\cdot2\pi r`

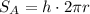
Now, we determine the radius of the base, that is:

`r=(2.6)/(2)\Rightarrow r=1.3`

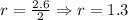
Now, we replace the values and solve for the surface area:

`\Rightarrow S_A=(4)\cdot(2)\pi(1.3)\Rightarrow S_A\approx32.7`

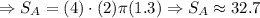
So, the surface area of the label on the can is approximately 32.7 squared inches.