Question

What is the voltage drop across point A and B?

Answer 1

We are asked to find the voltage drop at point A and B

Notice that point A and B have 3 resistors connected in parallel so the voltage across these 3 resistors will be the same.

First, we have to find the equivalent resistance of these 3 parallel resistors.

`\begin{gathered} R_(AB)=(1)/((1)/(R_1)+(1)/(R_2)+(1)/(R_3)) \\ R_(AB)=(1)/((1)/(120)+(1)/(60)+(1)/(30)) \\ R_(AB)=17.14\; \Omega \end{gathered}`

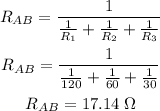
So, the resistance of the parallel resistors is 17.14

Now, we can simply use the voltage drop formula to find the voltage drop at point A and B

`\begin{gathered} V_(AB)=(R_(AB))/(R_(total))* V_{\text{in}} \\ V_(AB)=(R_(AB))/(R_(AB)+R_(CD))* V_{\text{in}} \end{gathered}`

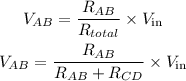
Where Vin is the input voltage that is 100 V

`\begin{gathered} V_(AB)=(17.14)/(17.14+100)*100 \\ V_(AB)=14.63\; V \end{gathered}`

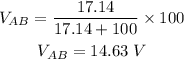
Therefore, there is a 14.63 V drop at point A and B