Question

you find the density of an object 4 times 1.3g/ml 1.25g/ml 1.17g/ml and 1.22g/ml now determine the percent deviation from the mean

Answer 1

Firstly we will determine the average or the mean of the objects density:

`\begin{gathered} Mean=(1.3g•mL^(-1)+1.25g•mL^(-1)+1.17g•mL^(-1)+1.22g•mL^(-1))/(4) \\ Mean=(4.94g•mL^(-1))/(4) \\ Mean=1.235 \end{gathered}`

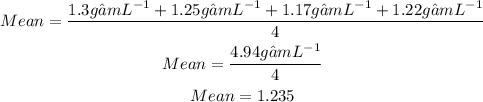
Now we will calculate the deviation. The deviation is how much is trial is different from the average. We take the absolute value so the answers can be positive:

`\begin{gathered} Trial\text{ }1:|1.3-1.235|=0.065 \\ Trial\text{ }2:|1.25-1.235|=0.015 \\ Trial\text{ }3:|1.17-1.235|=0.065 \\ Trial\text{ }4:|1.22-1.235|=0.015 \end{gathered}`

We will determine the average of the deviation:

`\begin{gathered} Deviation\text{ }mean=(0.065+0.015+0.065+0.015)/(4) \\ Deviation\text{ }mean=0.04 \end{gathered}`

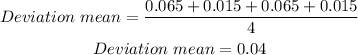
To determine the percent deviation we:

`\begin{gathered} \%\text{ }deviation=\frac{mean\text{ }deviation}{mean}*100 \\ \\ \%\text{ }deviation=(0.04)/(1.235)*100 \\ \\ \%\text{ }deviation=3.24\% \end{gathered}`

Answer: The percent deviation from the mean is 3.24%,