Question

I need help with this practice problem solving the subject is trig I have an additional picture that is the answer options, I will send this to you

Answer 1

Given

`f(x)=\tan x`

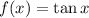
To fill the blanks.

Now,

The grpah of f(x)=tanx is given as,

Therefore, from the graph,

`\tan x=\tan (x+\pi)=\tan (x+2\pi)`

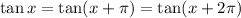
Then,

`\pi\text{ is the fundamental period of tanx.}`

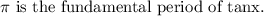
Also,

For x=0, tan(0)=0.

Therefore, the y-intercept is (0,0).

The points for the function f(x)=tanx is,

`\begin{gathered} x=(\pi)/(3),\text{ y=tan(}(\pi)/(3))=\sqrt[]{3} \\ x=(\pi)/(4),y=\tan (\pi)/(4)=1 \end{gathered}`

Since

`\tan (-A)=-\tan A`

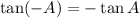
Then, the points of the graph y=tanx is,

`(-(\pi)/(3),-\sqrt[]{3}),(-(\pi)/(4),-1),(0,0),((\pi)/(3),\sqrt[]{3}),((\pi)/(4),1)`

Hence, the answer should be in the order,

i)

`\pi`

ii)

`(0,0)`

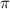
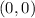
iii)

`(-(\pi)/(3),-\sqrt[]{3}),(-(\pi)/(4),-1),(0,0),((\pi)/(3),\sqrt[]{3}),((\pi)/(4),1)`