ANSWER
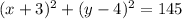
Step-by-step explanation
The equation of a circle is given by:

where (h, k) = center of the circle
r = radius of the circle
The center of a circle is the midpoint of the endpoints of the diameter of the circle. Hence, to find the center of the circle, we have to find the midpoint of the diameter:
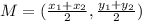
where (x1, y1) and (x2, y2) are the endpoints of the diameter.
Hence, the center of the circle is:
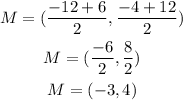
To find the radius of the circle, we have to find the distance between any endpoint of the circle and the center of the circle.
To do this apply the formula for distance between two points:
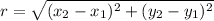
Therefore, the radius of the circle is:
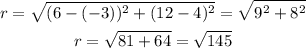
Hence, the equation of the circle is:
