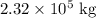Question

an ice has a volume of 8975 ft^3. what is the mass in kilograms of the iceberg? the density of ice 0.917 g/cm^3

Answer 1

The density is given by:

`\rho=(m)/(V)`

where V is the volume and m is the mass.

To determine the mass we have to solve the equation for m:

`m=\rho V`

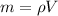
Now, before we can calculate the mass we have to convert the volume given to cubic meter, this comes from the fact that the density is given in g/cm^3 units. We have to remember that a ft is equal to 30.48 cm, then we have:

`8975ft^3(\frac{30.48\text{ cm}}{1\text{ ft}})(\frac{30.48\text{ cm}}{1\text{ ft}})(\frac{30.48\text{ cm}}{1\text{ ft}})=2.54*10^8`

Hence the volume of the iceberg is:

`2.54*10^8cm^3`

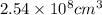
Now that we have the volume in the correct units we plug its value and the density in the equation for the mass above:

`\begin{gathered} m=2.54*10^8(0.917) \\ m=2.32*10^8 \end{gathered}`

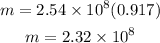
Hence the mass of the iceber is 2.32x10^8 g.

Therefore the mass of the iceberg in kilograms is:

`2.32*10^5\text{ kg}`