Question

Find the probability of at least 2 girls in 6 births. Assume that male and female births are equally likely and that the births are independent events.0.6560.1090.2340.891

Answer 1

We need to use Binomial Probability.

Of 6 births, we want to find the probability of at least 2 of them being girls.

To solve this, we need to find:

Probability of exactly 2 girls

Probability of exactly 3 girls

Probability of exactly 4 girls

Probability of exactly 5 girls

Probability of exactly 6 girls

If we add all these probabilities, we get the probability of at least 2 girls.

To find the probabilities, we can use the formula:

`_nC_r\cdot p^r(1-p)^(n-r)`

Where:

n is the number of trials (in this case, the number of total births)

r is the number of girls we want to find the probability

p is the probability of the event occurring

`_nC_r\text{ }is\text{ }the\text{ }combinatoric\text{ }`

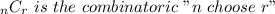
The formula for "n choose r" is:

`_nC_r=(n!)/(r!(n-r)!)`

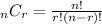
Then, let's find the probability of exactly 2 girls:

The probability of the event occurring is:

`P(girl)=(1)/(2)`

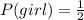
Because there is a 50% probability of being a girl or a boy.

let's find "6 choose 2":

`_6C_2=(6!)/(2!(6-2)!)=(720)/(2\cdot24)=15`

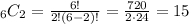
Now we can find the probability of exactly 2 girls:

`Exactly\text{ }2\text{ }girls=15\cdot((1)/(2))^2(1-(1)/(2))^(6-2)=15\cdot(1)/(4)\cdot((1)/(2))^4=(15)/(4)\cdot(1)/(16)=(15)/(64)`

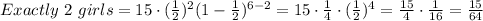
We need to repeat these calculations for exactly 3, 4, 5, and 6 girls:

Exactly 3 girls:

let's find "6 choose 3":

`_6C_3=(6!)/(3!(6-3)!)=(720)/(6\cdot6)=20`

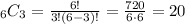
Thus:

`Exactly\text{ }3\text{ }girls=20\cdot((1)/(2))^3(1-(1)/(2))^(6-3)=20\cdot(1)/(8)\cdot(1)/(8)=(5)/(16)`

Exactly 4 girls:

"6 choose 4":

`_6C_4=(6!)/(4!(6-4)!)=(720)/(24\cdot2)=15`

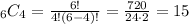
Thus:

`Exactly\text{ }4\text{ }girls=15\cdot((1)/(2))^4(1-(1)/(2))^(6-4)=15\cdot(1)/(16)\cdot(1)/(4)=(15)/(64)`

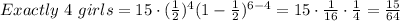
Exactly 5 girls:

"6 choose 5"

`_6C_5=(6!)/(5!(6-5)!)=(720)/(120)=6`

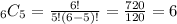
Thus:

`Exactly\text{ }5\text{ }girls=6\cdot((1)/(2))^5(1-(1)/(2))^(6-5)=6\cdot(1)/(32)\cdot(1)/(2)=(3)/(32)`

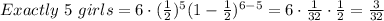
Exactly 6 girls:

"6 choose 6"

`_6C_6=(6!)/(6!(6-6)!)=(720)/(720\cdot0!)=(720)/(720)=1`

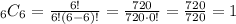
Thus:

`Exactly\text{ }6\text{ }girls=1\cdot((1)/(2))^6(1-(1)/(2))^(6-6)=(1)/(64)\cdot((1)/(2))^0=(1)/(64)`

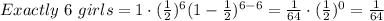
now, to find the answer we need to add these 5 values:

`(15)/(64)+(5)/(16)+(15)/(64)+(3)/(32)+(1)/(64)=(57)/(64)=0.890625`

To the nearest tenth, the probability of at least 3 girls is 0.891, thus, the last option is the correct one.