Question

The average American man consumes 9.6 grams of sodium each day. Suppose that the sodium consumption of American men is normally distributed with a standard deviation of 0.8 grams. Suppose an American man is randomly chosen. Let X = the amount of sodium consumed. Round all numeric answers to 4 decimal places where possible. a. What is the distribution of X? X - NO b. Find the probability that this American man consumes between 9.7 and 10.6 grams of sodium per day. C. The middle 10% of American men consume between what two weights of sodium? Low: High:

Answer 1

The variable of interest is

X: sodium consumption of an American male.

a) This variable is known to be normally distributed and has a mean value of μ=9.6grams with a standard deviation of δ=0.8gr

Any normal distribution has a mean = μ and the variance is δ², symbolically:

X~N(μ ,δ²)

For this distribution, we have established that the mean is μ=9.6grams and the variance is the square of the standard deviation so that: δ² =(0.8gr)²=0.64gr²

Then the distribution for this variable can be symbolized as:

X~N(9.6,0.64)

b. You have to find the probability that one American man chosen at random consumes between 9.7 and 10.6gr of sodium per day, symbolically:

`P(9.7\leq X\leq10.6)`

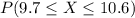
The probabilities under the normal distribution are accumulated probabilities. To determine the probability inside this interval you have to subtract the accumulated probability until X≤9.7 from the probability accumulated probability until X≤10.6:

`P(X\leq10.6)-P(x\leq9.7)`

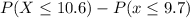
Now to determine these probabilities, we have to work under the standard normal distribution. This distribution is derived from the normal distribution. If you consider a random variable X with normal distribution, mean μ and variance δ², and you calculate the difference between the variable and ist means and divide the result by the standard deviation, the variable Z =(X-μ)/δ ~N(0;1) is determined.

The standard normal distribution is tabulated. Any value of any random variable X with normal distribution can be "converted" by subtracting the variable from its mean and dividing it by its standard deviation.

So to calculate each of the asked probabilities, you have to first, "transform" the value of the variable to a value of the standard normal distribution Z, then you use the standard normal tables to reach the corresponding probability.

`P(X\leq10.6)=P(Z\leq(10.6-9.6)/(0.8))=P(Z\leq1.25)`
`P(X\leq9.7)=P(Z\leq(9.7-9.6)/(0.8))P(Z\leq0.125)`

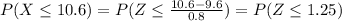
So we have to find the probability between the Z-values 1.25 and 0.125

`P(Z\leq1.25)-P(Z\leq0.125)`

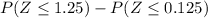
Using the table of the standard normal tables, or Z-tables, you can determine the accumulated probabilities:

`P(Z\leq1.25)=0.894`
`P(Z\leq0.125)=0.550`

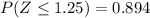
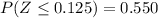
And calculate their difference as follows:

`0.894-0.550=0.344`

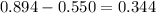
The probability that an American man selected at random consumes between 10.6 and 9.7 grams of sodium per day is 0.344

c. You have to determine the two sodium intake values ​​between which the middle 10% of American men fall. If "a" and "b" represent the values we have to determine, between them you will find 10% of the distribution. The fact that is the middle 10% indicates that the distance between both values to the center of the distribution is equal, so 10% of the distribution will be between both values and the rest 90% will be equally distributed in two tails "outside" the interval [a;b]

Under the standard normal distribution, the probability accumulated until the first value "a" is 0.45, so that:

`P(Z\leq a)=0.45`

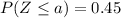
And the accumulated probability until "b" is 0.45+0.10=0.55, symbolically:

`P(Z\leq b)=0.55`

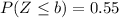
The next step is to determine the values under the standard normal distribution that accumulate 0.45 and 0.55 of probability. You have to use the Z-tables to determine both values:

The value that accumulates 0.45 of probability is Z=-0.126

To translate this value to its corresponding value of the variable of interest you have to use the standard normal formula:

`a=(X-\mu)/(\sigma)`

You have to write this expression for X

`\begin{gathered} a\cdot\sigma=X-\mu \\ (a\cdot\sigma)+\mu=X \end{gathered}`

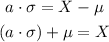
Replace the expression with a=-0.126, μ=9.6gr, and δ=0.8gr

`\begin{gathered} X=(a\cdot\sigma)+\mu \\ X=(-0.126\cdot0.8)+9.6 \\ X=-0.1008+9.6 \\ X=9.499 \\ X\approx9.5gr \end{gathered}`

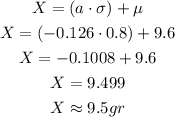
The value of Z that accumulates 0.55 of probability is 0.126, as before, you have to translate this Z-value into a value of the variable of interest, to do so you have to use the formula of the standard normal distribution and "reverse" the standardization to reach the corresponding value of x:

`\begin{gathered} b=(X-\mu)/(\sigma) \\ b\cdot\sigma=X-\mu \\ (b\cdot\sigma)+\mu=X \end{gathered}`

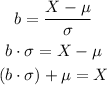
Replace the expression with b=0.126, μ=9.6gr, and δ=0.8gr and calculate the value of X:

`\begin{gathered} X=(b\cdot\sigma)+\mu \\ X=(0.126\cdot0.8)+9.6 \\ X=0.1008+9.6 \\ X=9.7008 \\ X\approx9.7gr \end{gathered}`

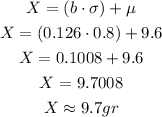
The values of sodium intake between which the middle 10% of American men fall are 9.5 and 9.7gr.