Question

Find the area to the right of x=71 under a normal distribution curve with the mean=53 and standard deviation=9

Answer 1

`Area=0.0228\text{ or 2.28\%}`

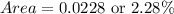
Step-by-step explanation:

We were given the following information:

This is a normal distribution curve

Mean = 53

Standard deviation = 9

We are to find the area right of x = 71

This is calculated as shown below:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ x=71 \\ \mu=53 \\ \sigma=9 \\ \text{Substitute these into the formula, we have:} \\ z=(71-53)/(9) \\ z=(18)/(9) \\ z=2 \end{gathered}`

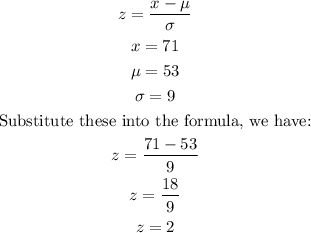
We will proceed to plot this on a graph as sown below:

The area to the right of x = 71 (highlighted in red above) is given by using a Standard z-score table:

`\begin{gathered} =1-0.9772 \\ =0.0228 \\ =2.28\text{\%} \end{gathered}`

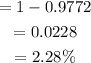
Therefore, the area that lies to the right of x = 71 is 0.0228 or 2.28%