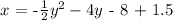Question

Write the equation for a parabola with a focus at (1,-4) and a directrix at x= 2.x=?

Answer 1

The basic form of the equation is;

4p (x- h)= (y - k)²

where (h, k) is the vertex and p is the distance from the vertex to either of its directrix or the focus

But, focus is = (1, -4) adn directrix = 2

So, the perpendicular point is :

(1.5 , -4)

p = -0.5

Putting all the values into the formula

4p (x- h)= (y - k)²

4(-0.5)(x - 1.5) = (y - (-4)²

simplify

-2(x - 1.5) = (y + 4)²

-2(x - 1.5) = y² + 8y + 16

Divide through the equation by -2

x - 1.5 = (-1/2) y² - 4y - 8

Add 1.5 to both-side of the equation

`x\text{ = -}(1)/(2)y^2-4y\text{ - 8 + 1.5}`

`x=-(1)/(2)y^2-4y\text{ - 6.5}`