Question

A soccer ball is kicked on a field and follows the path of a parabola. It reaches a maximum height of 80 feet above the ground after traveling 160 feet from where it was kicited.a) Draw a diagram to represent this situation.b) Write an exact equation in vertex form to model this situation.c) Suppose there is a 30 feet tree 280 feet from where the ball was kicked. Will the ball sail over the tree? If yes, by how much? If not, by how much?

Answer 1

a) We will draw the situation.

b) Considering the theory, the vertex of a parabola is represented in (h,k) where h is the x-coordinate, in this case, if our parabola has an amplitude of x=320feet then h=320/2=160feet, and k is the highest y-coordinate 80 feet. So the equation is:

`\begin{gathered} y=a(x-h)^2+k \\ y=a(x-160)^2+80 \end{gathered}`

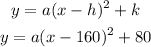
We have to know the value for a, so we will use a point to replace it in the equation and with that, we will know the value, so in x=0 the y-value is 0 too so:

`\begin{gathered} 0=a(0-160)^2+80 \\ a(-160)^2=-80 \\ a=-(80)/(25600)=-(1)/(320) \end{gathered}`

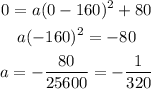
So the equation is:

`y=-(1)/(320)(x-160)^2+80`

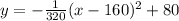
c. To know the answer to this question we will have to replace x=280feet with the y value we will know if at the moment the ball can go over the tree or if it would crash into it.

`\begin{gathered} y=-(1)/(320)(280-160)^2+80 \\ y=35feet \end{gathered}`

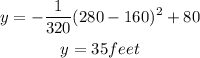
At that point, the ball would be 35 feet up so if it could pass over the tree 5 feet higher.