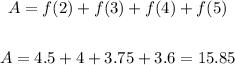Question

Use the figures to estimate the area under the curve for the given function using four rectangles.

Answer 1

To calculate the area for the upper (left) graph, we can use x = 1, 2, 3 and 4 to find the upper limit of each rectangle:

`\begin{gathered} f(1)=(3)/(1)+3=6\\ \\ f(2)=(3)/(2)+3=4.5\\ \\ f(3)=(3)/(3)+3=4\\ \\ f(4)=(3)/(4)+3=3.75 \end{gathered}`

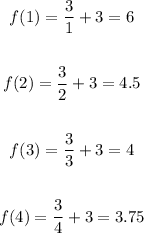
Since the x-interval of each rectangle is 1 unit, the area of each rectangle is given by its y-value, so we have:

`\begin{gathered} A=f(1)+f(2)+f(3)+f(4)\\ \\ A=6+4.5+4+3.75=18.25 \end{gathered}`

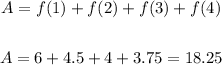
Now, for the bottom (right) graph, the limits of the rectangles are x = 2, 3, 4 and 5.

So, let's find the value of f(5):

`f(5)=(3)/(5)+3=3.6`

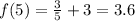
So the area is given by:

`\begin{gathered} A=f(2)+f(3)+f(4)+f(5)\\ \\ A=4.5+4+3.75+3.6=15.85 \end{gathered}`