Question

A rectangle has a length of 9 inches and a widt of 5 inches whose sides are changing. The length is increasing by 3 in/sec and the width is shrinking at 9 in/sec. What is the rate of change of the perimeter?

Answer 1

Given:

A rectangle has a length of 9 inches and a width of 5 inches whose sides are changing. The length is increasing by 3 in/sec and the width is shrinking at 9 in/sec.

To find:

The rate of change of the perimeter.

Solution:

It is known that the perimeter of the rectangle is twice the sum of length and width.

`P=2(l+w)`

DIfferentiate the perimeter with respect to t:

`(dP)/(dt)=2((dl)/(dt)+(dw)/(dt))`

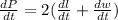
From the given information:

`\begin{gathered} (dP)/(dt)=2(3-9) \\ =2(-6) \\ =-12 \end{gathered}`

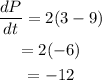
Thus, the perimeter of the rectangle is decreasing at the rate of 12 inches per second.