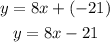Question

A. Find the equation of the L line that intersects graph C at point A (2, -5). B. Find the line equation with the coefficient of direction equal to -10 and touch and graph C

Answer 1

Graph C has a function

`f(x)=2x^3-16x+11`

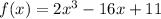
Since the line L intersects the graph at the point, A (2, -5)

To find the slope of the line we will differentiate the f(x) and substitute x by 2

`\begin{gathered} f^(\prime)(x)=2(3)x^(3-1)-16x^(1-1)+0 \\ f^(\prime)(x)=6x^2-16 \\ m=6(2)^2-16 \\ m=24-16 \\ m=8 \end{gathered}`

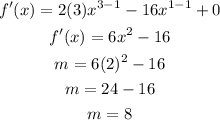
The slope of the line is 8, substitute it in the form of the linear equation

`\begin{gathered} y=mx+b \\ y=8x+b \end{gathered}`

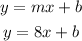
To find b substitute x by 2 and y by -5

`\begin{gathered} -5=8(2)+b \\ -5=16+b \end{gathered}`

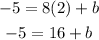
Subtract 16 from both sides to find b

`\begin{gathered} -5-16=16-16+b \\ -21=b \end{gathered}`

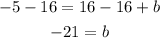
Then the equation of the line is

`\begin{gathered} y=8x+(-21) \\ y=8x-21 \end{gathered}`