1 Answer

Ask a Question

Hooligancat · Answer 1 · 2023-05-27T01:15:59+0000

Since the resistances are in parallel, the voltage in each one is the same, so:

a. V1 = 60 V

b. V2 = 60 V

c. V3 = 60 V

d.

The total resistance of parallel resistances can be calculated with the formula below:

$\begin{gathered} (1)/(RT)=(1)/(R1)+(1)/(R2)+(1)/(R3)\\ \\ RT=(R1\cdot R2\cdot R3)/(R1R2+R2R3+R1R3)\\ \\ RT=\frac{11\cdot17\cdot12}{11\cdot17+17\operatorname{\cdot}12+11\operatorname{\cdot}12}\\ \\ RT=(2244)/(523)\\ \\ RT=4.29\text{ ohms} \end{gathered}$

e.

The total current is given by the voltage divided by the total resistance:

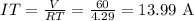
$IT=(V)/(RT)=(60)/(4.29)=13.99\text{ A}$

The current in each resistor is given by the voltage divided by the resistance:

f.

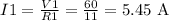
$I1=(V1)/(R1)=(60)/(11)=5.45\text{ A}$

g.

$I2=(V2)/(R2)=(60)/(17)=3.53\text{ A}$

h.

$I3=(V3)/(R3)=(60)/(12)=5\text{ A}$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions