
1) We can do this by listing all the factors of -1, and the leading coefficient 6. So, we can write them as a ratio this way:
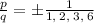
Note that p stands for the constant and q the factors of that leading coefficient
2) Now, let's test them by plugging them into the polynomial. If it is a rational root it must yield zero:

3) So the possible roots are:
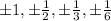
But there are no actual rational roots.