Answer:
(x, y) = (5.5, 2)
Step-by-step explanation:
The coordinates of a point that divide the segment from point (x1, y1) to (x2, y2) into a ratio of a:b can be found using the following equations:

So, replacing (x1, y1) by (3, -3), (x2, y2) by (7, 5) and the ratio a:b by 5:3, we get that the coordinates of the point are:
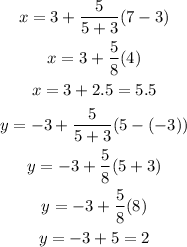
Therefore, the coordinates of the point are (x, y) = (5.5, 2)