Question

Trying to solve this problem kind of having a hard time

Answer 1

Future Value of an Investment

The formula to calculate the future value (FV) of an investment P for t years at a rate r is:

`FV=P\mleft(1+(r)/(m)\mright)^(m\cdot t)`

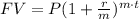
Where m is the number of compounding periods per year.

Leyla needs FV = $7000 for a future project. She can invest P = $5000 now at an annual rate of r = 10.5% = 0.105 compunded monthly. This means m = 12.

It's required to find the time required for her to have enough money for her project.

Substituting:

`\begin{gathered} 7000=5000(1+(0.105)/(12))^(12t) \\ \text{Calculating:} \\ 7000=5000(1.00875)^(12t) \end{gathered}`

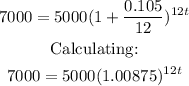
Dividing by 5000:

`(7000)/(5000)=(1.00875)^(12t)=1.4`

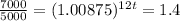
Taking natural logarithms:

`\begin{gathered} \ln (1.00875)^(12t)=\ln 1.4 \\ \text{Operating:} \\ 12t\ln (1.00875)^{}=\ln 1.4 \\ \text{Solving for t:} \\ t=\frac{\ln 1.4}{12\ln (1.00875)^{}} \\ t=3.22 \end{gathered}`

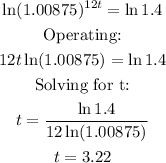
It will take 3.22 years for Leila to have $7000