In order to corroborate that the points belong to the equation, we must subtitute the points into the equation.
If we substitute the points from option A, we get
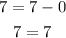
for (1,8), we have
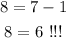
then, option A is false.
Now, if we substitute the points in option B, for point (2,5), we have
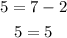
which is correct. Now, for point (-1.8) we obtain
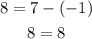
Since all the points fulfil the equation, then option B is an answer.
Lets continue with option C and D.
If we substitute point (1,8) from option C, we have
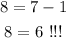
then, option C is false.
If we substite point (4,11) from option D, we get
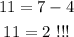
then, option D is false.
Therefore, the answer is option B.