
Step-by-step explanation:
The y-intercept is the value of y when x = 0
To identify y-intercept on a graph, we will check for the the value of y when the line crosses the y axis
From the graph, the line crosses the y axis at y = 6
Hence, the y-intercept is 6
To get the slope, we will pick any two points on the line.
Using points (0, 6) and (4, 0)
Applying the slope formula:
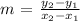
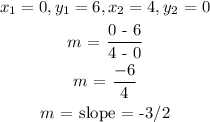
NOTE: the slope is negative because it is going from up to down (moving downwards)
The equation of slope in intercept form: y = mx + b
m = slope = -3/2
b = y-intercept = 6
The equation in y-intercept becomes:
