Question

Find the horizontal and vertical components for a vector round to the nearest tenth

Answer 1

Step 1:

In this question, we are given the following:

Step 2:

The details of the solution are as follows:

The horizontal component of a vector having:

`\text{ a magnitude of v and a direction of }\theta\text{ = v cos }\theta`

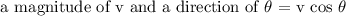
The vertical component of a vector having:

`a\text{ magnitude of v and direction of }\theta\text{ = v sin}\theta`

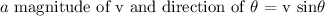
Then, with the information above, the horizontal component of a vector having a magnitude of 15 and a direction of 210 degrees:

`\begin{gathered} \text{Horizontal component = 15 x cos 210}^{\text{ 0}}=\text{ 15 x -0.8860 = -12.99}\approx\text{ -13.0 } \\ \text{Taking the absolute value, we have } \\ \text{Horizontal component = 13.0 units ( to the nearest tenth)} \end{gathered}`

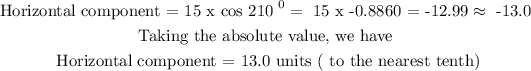
The vertical component of a vector having a magnitude of 15 and a direction of 210 degrees:

`\begin{gathered} vertical\text{ component = 15 x sin 210}^{\text{ 0}}=\text{ 15 x -0.5 = -7.5 } \\ \text{Taking the absolute value, we have } \\ Vertical\text{component = 7.5 units ( to the nearest tenth)} \\ \\ \text{Hence the horizontal and vertical component of the vector =} \\ (\text{ 13. 0 , 7. 5 ) ( to the nearest tenth)} \end{gathered}`