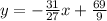Given:
Given the function
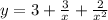
and a point x = 3.
Required: Equation of the line tangent to y at x = 3.
Step-by-step explanation:
The derivative of a function is he slope of the tangent line of the function at a given point. So, finding the derivative gives the slope of the tangent line.

Substitute 3 for x into the derivative.
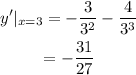
Therefore, the slope of the tangent line is -31/27.
Substitute 3 for x into y.
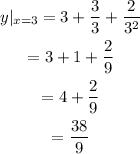
(3, 38/9) is the only point on the tangent line where it intersects the original graph.
Plug these coordinates along with slope into the general point-slope form to find the equation.
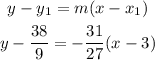
Solving for y will give the equation in slope-intercept form.
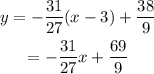
Final Answer: The equation of the tangent line is