Question

Given the parametric equations x = 7cos θ and y = 5sin θ, which of the following represents the curve and its orientation?

Answer 1

We have the following parameters

`\begin{gathered} x=7cos\theta \\ y=5sin\theta \end{gathered}`

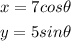
the general equation of a circle with center (0,0) is the following,

`x^2+y^2=r^2`

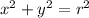
Let's use the following tigonometric identity,

`sin^2\theta+cos^2\theta=1`

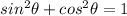
solving for cos and sin in the equations we are given,

`cos\theta=(x)/(7),sin\theta=(y)/(5)`

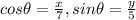
replace,

`((y)/(5))^2+((x)/(7))^2=1`

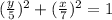
Since we have two different numbers in the denominator, this is not a circle equation but an elipse, of the form,

`(y^2)/(a^2)+(x^2)/(b^2)=1`

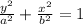
where,

a is the vertex and,

b is the covertex

thus, in the x axis, the vertex is 7 and the y-axis the covertex is 5

Now, let's determine the direction by replacing

when Θ = 0 , then x = 7*cos0 = 7*1 = 7 , and y = 5*sin0 = 5*0 = 0

when Θ = 90° or π/2 , then x = 7*cos90° = 7*0 = 0 , and y = 5sin90° = 5*1 = 5

If we draw this, we can see that the direction is counterclockwise as in the bottom right image.